搜索树

二叉搜索树

• 左子树小于根结点
• 右子树大于根结点
• 若以中序遍历二叉搜索树，将得到递增有序序列

存储方式

代码

定义集合项

typedef struct entry
{
    KeyType Key;
    DataType Data;
}T

定义结点

typedef struct btnode
{
    T Element;
    struct btnode *lChild, *rChild;
}BTNode;

定义搜索树

typedef struct btree
{
    BTNode *root;
}BTree;

搜索

步骤

查找关键字$x$

1. 二叉树为空，搜索失败
2. 将$x$与根结点比较
   • $k$小于该结点，搜索左子树
   • $k$大于该结点，搜索右子树
   • $k$等于该结点，搜索成功

代码

递归算法

BTNode *Find(BTNode *p,KeyType k)
{
    if(!p)
        return NULL; // 搜索失败
    if(k == p->element.key)
        return p; // 搜索成功
    if(k < p->element.key)
        return Find(p->lChild,k);
    return Find(p->rChild,k);
}
BOOL BtSearch(BTree Bt,KeyType k,T *x)
{
    BTNode *p = Find(Bt.root,k);
    if(p)
    {
        *x = p->element;
        return TRUE;
    }
    return FALSE;
}

迭代算法

BOOL BtSearch(Btree Bt,KeyType k,T *x)
{
    BTNode *p = Bt.Root; // 从根结点出发
    while(p)
    {
        if(k < p->element.key) // 从左分支继续向下搜索
            p = p->lChild;
        else if(k > p->element.key) // 从右分支继续向下搜索
            p = p->rChild;
        else
        {
            *x = p->element; // 搜索成功
            return TRUE;
        }
    }
    return FALSE;
}

插入

• 向下搜索$x$
• 搜索失败处插入$x$

BOOL Insert(Btree *bt, T x)
{
    BTNode *p = bt->root, *q, *r; // p:从根节点向下搜索 q:记录搜索失败上一层结点
    KeyType k = x.key;
    while(p)
    {
        q = p;
        if(k < p->element.key)
            p = p->lChild;
        else if(k > p->element.key)
            p = p->rChild;
        else
            return FALSE;
    }
}

删除

删除叶子结点

直接删

1. 将待删除结点双亲结点指向NULL
2. 释放待删除结点

删除有一个孩子结点

爷带孙

1. 待删除结点的双亲结点指向待删除结点的孩子
2. 释放待删除结点

删除有两个孩子结点

1. 从后代选择一个覆盖待删除结点
   • 保持二叉搜索树有序性==左孩子$\leq$代替这$\leq$右孩子==
   • 容易删除==只有一个孩子或没有孩子==
2. 删除重复的代替者

   代替者选择方法

• 选择其中序遍历的直接前驱
  • 为左子树最大值
  • 一定没有右孩子
• 选择其中序遍历的直接后驱
  • 为右子树最小值
  • 一定没有左孩子

二叉平衡树

定义

• 二叉搜索树
• 左右子树高度差$h’\leq{1}$
• 左右子树都是二叉平衡树

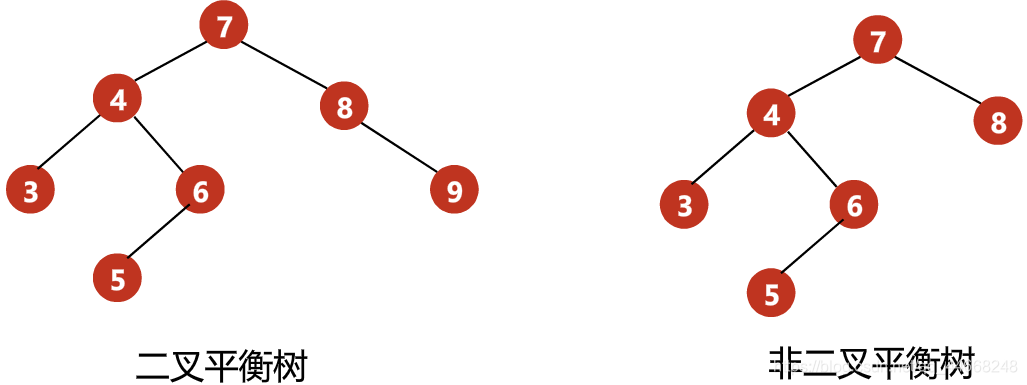
• 平衡因子——左子树与右子树高度差$h_{left}-h_{right}$

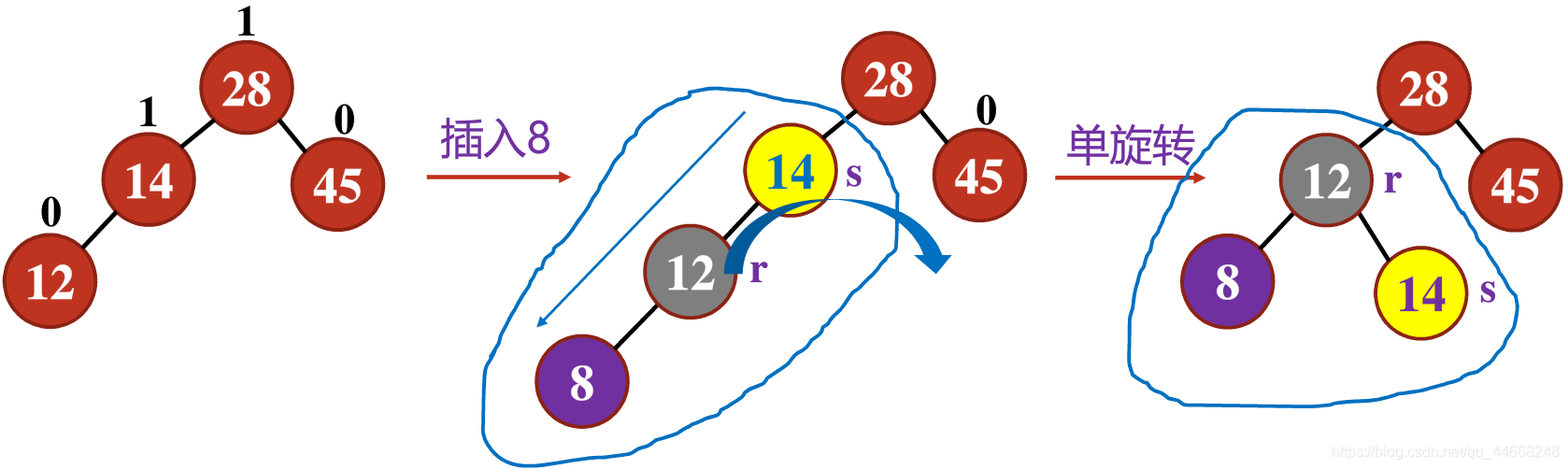
二叉平衡树插入

• 先按照普通二叉搜索树插入

• 若不平衡，则进行调整

  • 先找到平衡因子超过$1$的根结点$s$

    1. $LL/RR$类型——单旋转

       新结点插入$s$的左/右结点

       

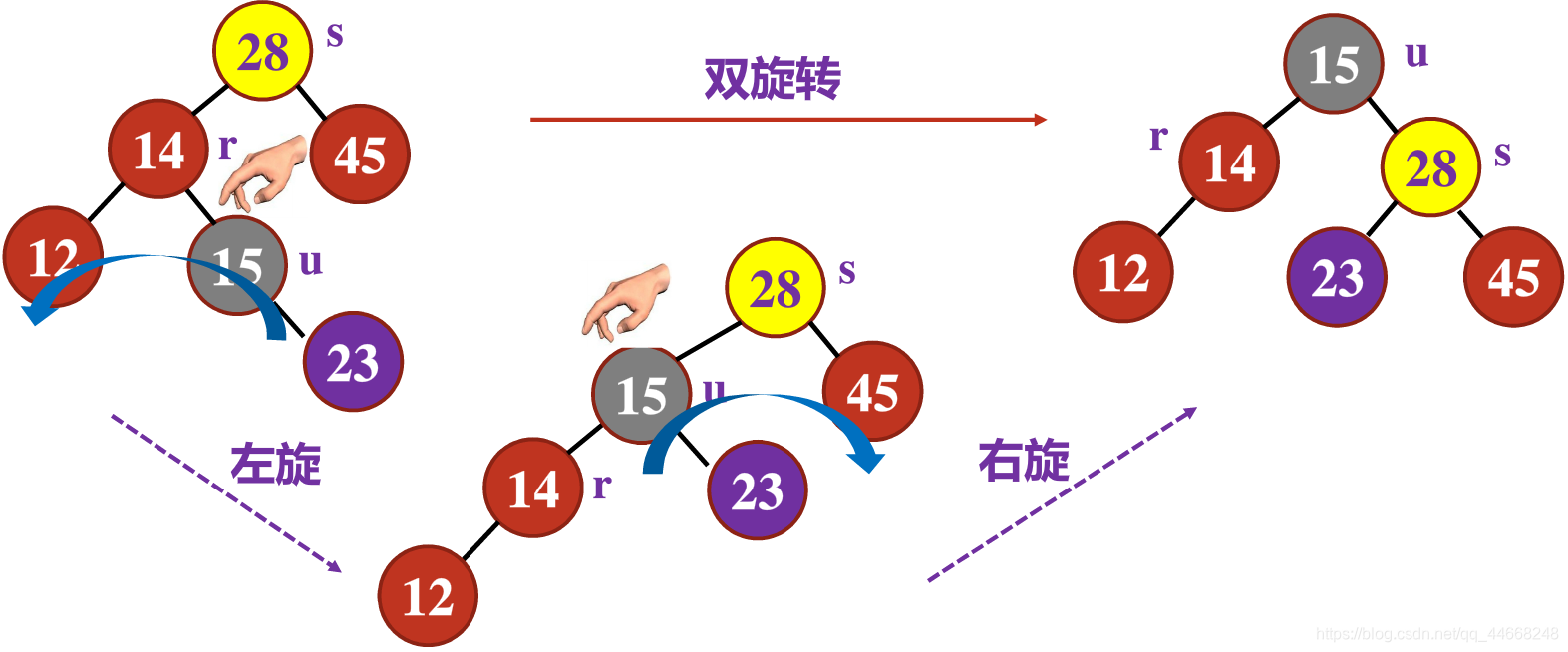
    2. $LR/RL$类型——双旋转

       

m叉搜索树

存储方式

• 空树——失败结点

• ==失败结点不是叶子节点==

• 根结点最多$m$棵子树

  
  • $k_i$是元素关键字
  • $P_i$是指向子树的指针
  • $n$为该结点元素个数，$1{\leq}n{\leq}m$

• 子树$P_i$所有关键字大于$K_i$，小于$K_{i+1}$

• 子树$P_0$所有关键字值小于$K_1$

  子树$P_n$上所有关键字大于$K_n$

• 子树$P_i(0{\leq}i{\leq}n)$也是$m$叉二叉树

• 结点最多存放_m-1_个元素和_m_个指针

• 结点里元素个数比包含指针少$1$

性质

1. 高度为$h$的$m$二叉树最多$m^h-1$个元素

   高度为$h$的$m$二叉树最多$\dfrac{m^h-1}{m-1}$个结点

2. 含有$N$个元素的$m$叉搜索树高度$h$满足$h{\leq}log_m(N+1)$

B-树

定义

• 或者为空树
• 或满足$m$叉搜索树
  • 根结点至少两个孩子==可以只有一个元素==
  • 除根结点和失败结点所有结点**至少$\dfrac{m}{2}$**个孩子==确保B-树不会退化为单支树==
  • 所有失败结点在同一层==考虑平衡性==

判定性质

• 一个结点最多$m$个孩子，$m-1$个关键字
• 除根结点与失败结点每个结点至少$\dfrac{m}{2}$个孩子，$\dfrac{m}{2}-1$个关键字
• 根结点最少2个孩子
• 失败结点均在同一层，失败结点的双亲是叶子结点

判定方法

1. 失败结点是否在同一层
2. 根结点是否至少$2$个孩子
3. 确定$m$并计算$\dfrac{m}{2}$
4. 查看除根结点与失败者外所有结点的孩子数量是否少于$\dfrac{m}{2}$

性质

• $N=s-1$

  $s$——失败点总数

  $N$——$B-$树失败点总数

• 含有$N$个元素的$m$阶$B-$树高度$h$：$h{\leq}1+log_{\frac{m}{2}}{\dfrac{N+1}{2}}$

搜索

1. $B-$树中找结点，执行访问磁盘次数最多$log_{\frac{m}{2}}{\dfrac{N+1}{2}}$
2. 结点中找关键字

插入/删除

插入

步骤

1. 搜索待插入元素

   若已存在，则插入失败

2. 插入停留的失败结点的叶子结点中

3. 将结点分为{$1$~${\dfrac{m}{2}-1}$}、{$\dfrac{m}{2}$}、{${\dfrac{m}{2}}$~$m$}

4. 将{$\dfrac{m}{2}$}和其指针插入其双亲结点

   • 根结点会向上形成一个新的根结点

删除

步骤

1. 叶子结点直接删除

2. 否则以其右子树最小元素替换

3. 如发生下溢出，则若其左右兄弟有多于$\dfrac{m}{2}$个元素，则向其接一个元素

4. 没有富余兄弟，与兄弟合并且将两结点之间元素下移

   

   总结

考点

B-树性质

内容

• 高度为$h$的$m$二叉树最多$m^h-1$个元素

  高度为$h$的$m$二叉树最多$\dfrac{m^h-1}{m-1}$个结点

• 含有$N$个元素的$m$叉搜索树高度$h$满足$h{\leq}log_m(N+1)$

• $N=s-1$

  $s$——失败点总数

  $N$——$B-$树失败点总数

• 每个结点至多$m$个孩子，至少$[\dfrac{m}{2}]$个孩子

• 含有$N$个元素的$m$阶$B-$树高度$h$：$h{\leq}1+log_{\frac{m}{2}}{\dfrac{N+1}{2}}$

二叉搜索树插入删除